Policy Learning and Evaluation with Randomized Quasi-Monte Carlo
Summary
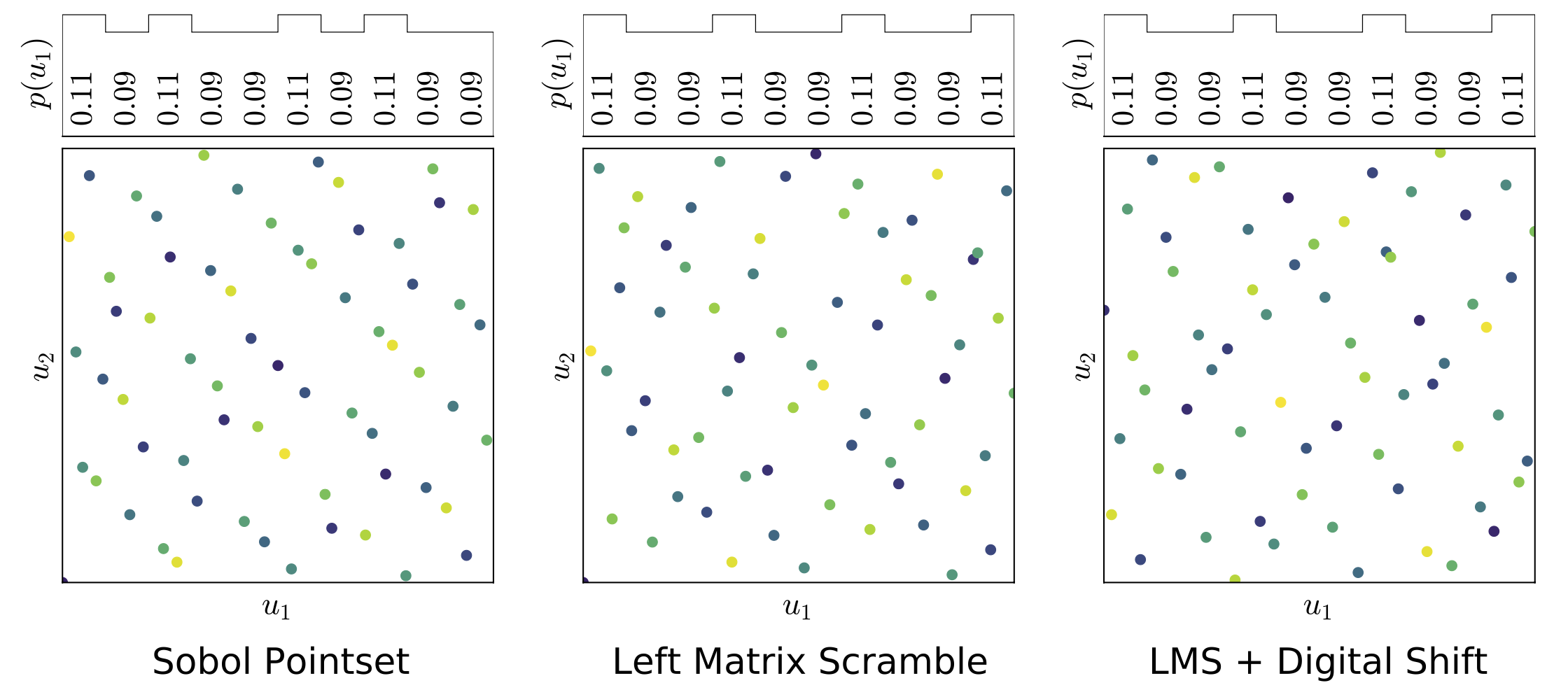
Reinforcement learning constantly deals with hard integrals, for example when computing expectations in policy evaluation and policy iteration. These integrals are rarely analytically solvable and typically esimated with the Monte Carlo method, which induces high variance in policy values and gradients. In this work, we propose to replace Monte Carlo samples with low-discrepancy point sets. We combine policy gradient methods with Randomized Quasi-Monte Carlo, yielding variance-reduced formulations of policy gradient and actor-critic algorithms. These formulations are effective for policy evaluation and policy improvement, as they outperform state-of-the-art algorithms on standardized continuous control benchmarks. Our empirical analyses validate the intuition that replacing Monte Carlo with Quasi-Monte Carlo yields significantly more accurate gradient estimates.
Code
Available at: github.com/seba-1511/qrl
public double[][] sample(int pow, int dim) {
MRG32k3a stream = new MRG32k3a();
int n_samples = (int)Math.pow(2, pow);
double[][] pointset = new double[n_samples][dim];
DigitalNetBase2 p = new SobolSequence(pow, 31, dim);
p.leftMatrixScramble(stream);
p.addRandomShift(stream);
PointSetIterator point_stream = p.iterator ();
for (int i = 0; i < n_samples; ++i) {
point_stream.nextPoint(pointset[i], dim);
}
return pointset;
}Reference
Please cite this work as
S. M. R. Arnold, P. L’Ecuyer, L. Chen, Y. Chen, F. Sha, Policy Learning and Evaluation with Randomized Quasi-Monte Carlo. AISTATS 2022.
or with the following BibTex entry.
@misc{arnold2019project,
title={Policy Learning and Evaluation with Randomized Quasi-Monte Carlo},
author={Arnold, S\'ebastien M. R. and L'Ecuyer, Pierre and Chen, Liyu and Chen, Yi-fan and Sha, Fei},
year={2022},
booktitle={Proceedings of The 25th International Conference on Artificial Intelligence and Statistics},
volume={131},
series={Proceedings of Machine Learning Research},
publisher={PMLR},
}Contact
Séb Arnold - seb.arnold@usc.edu
Using RQMC to reduce the variance in reinforcement learning.
VenuePeople
Resources