Autograd¶
Autograd is now a core torch package for automatic differentiation. It uses a tape based system for automatic differentiation.
In the forward phase, the autograd tape will remember all the operations it executed, and in the backward phase, it will replay the operations.
Variable¶
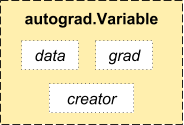
In autograd, we introduce a Variable class, which is a very thin
wrapper around a Tensor. You can access the raw tensor through the
.data attribute, and after computing the backward pass, a gradient
w.r.t. this variable is accumulated into .grad attribute.
Variable
There’s one more class which is very important for autograd
implementation - a Function. Variable and Function are
interconnected and build up an acyclic graph, that encodes a complete
history of computation. Each variable has a .grad_fn attribute that
references a function that has created a function (except for Variables
created by the user - these have None as .grad_fn).
If you want to compute the derivatives, you can call .backward() on
a Variable. If Variable is a scalar (i.e. it holds a one element
tensor), you don’t need to specify any arguments to backward(),
however if it has more elements, you need to specify a grad_output
argument that is a tensor of matching shape.
import torch
from torch.autograd import Variable
x = Variable(torch.ones(2, 2), requires_grad=True)
print(x) # notice the "Variable containing" line
print(x.data)
print(x.grad)
print(x.grad_fn) # we've created x ourselves
Do an operation of x:
y = x + 2
print(y)
y was created as a result of an operation, so it has a grad_fn
print(y.grad_fn)
More operations on y:
z = y * y * 3
out = z.mean()
print(z, out)
Gradients¶
let’s backprop now and print gradients d(out)/dx
out.backward()
print(x.grad)
By default, gradient computation flushes all the internal buffers
contained in the graph, so if you even want to do the backward on some
part of the graph twice, you need to pass in retain_variables = True
during the first pass.
x = Variable(torch.ones(2, 2), requires_grad=True)
y = x + 2
y.backward(torch.ones(2, 2), retain_graph=True)
# the retain_variables flag will prevent the internal buffers from being freed
print(x.grad)
z = y * y
print(z)
just backprop random gradients
gradient = torch.randn(2, 2)
# this would fail if we didn't specify
# that we want to retain variables
y.backward(gradient)
print(x.grad)
Total running time of the script: ( 0 minutes 0.000 seconds)